Bilangan bulat – Sebuah konsep matematika yang mungkin terlihat sederhana, namun ternyata punya peran penting dalam kehidupan kita. Dari menghitung uang di dompet hingga memahami suhu di luar, bilangan bulat selalu ada di sekitar kita. Tapi, apa sebenarnya bilangan bulat itu? Bagaimana kita menggunakannya dalam kehidupan sehari-hari? Yuk, kita jelajahi dunia bilangan bulat bersama-sama!
Bilangan bulat merupakan himpunan angka yang tidak memiliki komponen pecahan atau desimal. Artinya, bilangan bulat hanya terdiri dari angka utuh, baik positif maupun negatif, termasuk nol. Bayangkan sebuah garis lurus yang terbagi menjadi dua bagian: bagian positif di sebelah kanan nol, dan bagian negatif di sebelah kiri nol. Setiap angka pada garis ini, termasuk nol, adalah bilangan bulat. Konsep bilangan bulat ini menjadi dasar bagi berbagai ilmu pengetahuan dan teknologi yang kita gunakan saat ini.
Menjelajahi Dunia Bilangan Bulat: Definisi dan Representasinya

Mengenal Lebih Dekat: Definisi Bilangan Bulat
Bilangan bulat, seperti yang telah disinggung sebelumnya, adalah angka utuh tanpa komponen pecahan. Contohnya, 5, -3, 0, dan 100 adalah bilangan bulat. Sebaliknya, 3.14, 1/2, dan √2 bukan bilangan bulat karena memiliki komponen pecahan atau desimal.
Bilangan bulat dapat dibagi menjadi tiga jenis:
- Bilangan Asli: Bilangan bulat positif yang dimulai dari 1, seperti 1, 2, 3, 4, dan seterusnya. Bilangan asli digunakan untuk menghitung objek, seperti jumlah apel dalam keranjang atau jumlah siswa di kelas.
- Bilangan Nol: Bilangan yang mewakili ketiadaan atau tidak adanya sesuatu. Bilangan nol berada di tengah garis bilangan dan memisahkan bilangan positif dan negatif.
- Bilangan Negatif: Bilangan bulat yang terletak di sebelah kiri nol pada garis bilangan, seperti -1, -2, -3, -4, dan seterusnya. Bilangan negatif sering digunakan untuk menunjukkan kekurangan atau penurunan, seperti suhu di bawah titik beku atau saldo bank yang minus.
Melihat Bilangan Bulat dengan Lebih Jelas: Representasi Visual
Garis bilangan merupakan alat visual yang membantu kita memahami konsep bilangan bulat. Garis bilangan adalah garis lurus yang terbagi menjadi bagian-bagian yang sama, dengan titik nol sebagai pusatnya. Bilangan bulat positif terletak di sebelah kanan nol, sedangkan bilangan bulat negatif terletak di sebelah kiri nol. Setiap titik pada garis bilangan mewakili bilangan bulat tertentu.
Contohnya, titik yang terletak tiga satuan ke kanan nol mewakili bilangan bulat positif 3, sedangkan titik yang terletak dua satuan ke kiri nol mewakili bilangan bulat negatif -2. Garis bilangan memudahkan kita untuk membandingkan bilangan bulat, menentukan urutannya, dan melakukan operasi matematika.
Bermain dengan Bilangan Bulat: Operasi Matematika
Menjelajahi Penjumlahan dan Pengurangan: Operasi Dasar Bilangan Bulat
Penjumlahan dan pengurangan merupakan operasi matematika dasar yang dapat diterapkan pada bilangan bulat. Penjumlahan adalah proses menggabungkan dua bilangan bulat untuk mendapatkan jumlah totalnya, sedangkan pengurangan adalah proses mengurangi satu bilangan bulat dari bilangan bulat lainnya untuk mendapatkan selisihnya.
Ilustrasi dengan Garis Bilangan: Memvisualisasikan Penjumlahan dan Pengurangan
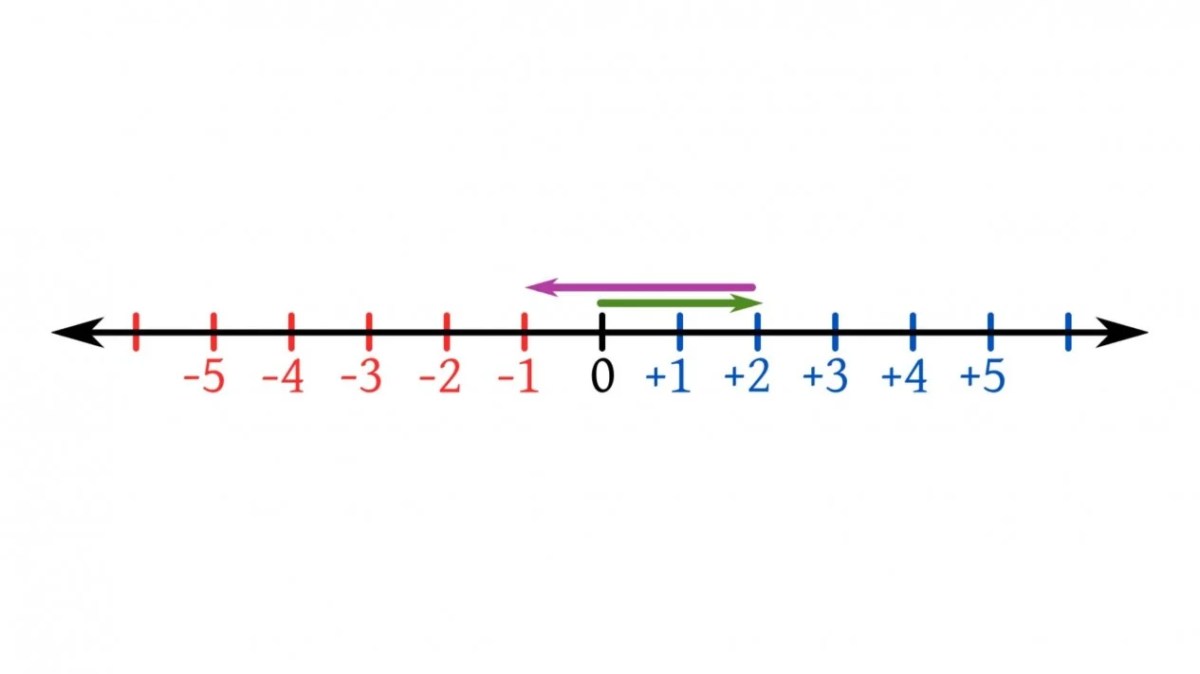
Garis bilangan dapat digunakan untuk memvisualisasikan penjumlahan dan pengurangan bilangan bulat. Misalnya, untuk menjumlahkan 2 dan 3, kita mulai dari titik 2 pada garis bilangan dan bergerak tiga satuan ke kanan. Titik akhir kita adalah 5, yang merupakan hasil penjumlahan 2 dan 3.
Untuk mengurangi 3 dari 5, kita mulai dari titik 5 pada garis bilangan dan bergerak tiga satuan ke kiri. Titik akhir kita adalah 2, yang merupakan hasil pengurangan 3 dari 5.
Ngomongin soal bilangan bulat, rasanya kayak lagi ngeliat peta Jalur Rempah, deh! Jalur Rempah itu kan menghubungkan berbagai tempat, dan bilangan bulat juga bisa menghubungkan berbagai konsep matematika. Bayangin, kalau kita mau ngitung berapa kapal yang lewat di Jalur Rempah, kita butuh bilangan bulat.
Begitu juga kalau kita mau ngitung berapa keuntungan yang didapat dari perdagangan rempah, bilangan bulat jadi kunci utamanya. Jadi, bilangan bulat tuh penting banget, kayak Jalur Rempah yang ngebentuk koneksi antar negara.
Sifat-sifat Penjumlahan dan Pengurangan: Aturan yang Mengatur Operasi
Penjumlahan dan pengurangan bilangan bulat memiliki beberapa sifat penting, yaitu:
- Sifat Komutatif Penjumlahan: Urutan penjumlahan tidak memengaruhi hasilnya. Misalnya, 2 + 3 = 3 + 2.
- Sifat Asosiatif Penjumlahan: Cara mengelompokkan bilangan dalam penjumlahan tidak memengaruhi hasilnya. Misalnya, (2 + 3) + 4 = 2 + (3 + 4).
- Sifat Identitas Penjumlahan: Penjumlahan bilangan bulat dengan nol menghasilkan bilangan bulat itu sendiri. Misalnya, 5 + 0 = 5.
- Sifat Invers Penjumlahan: Setiap bilangan bulat memiliki invers aditif, yaitu bilangan bulat yang jika dijumlahkan dengannya akan menghasilkan nol. Misalnya, invers aditif dari 5 adalah -5, karena 5 + (-5) = 0.
Menjelajahi Perkalian dan Pembagian: Operasi Lanjutan Bilangan Bulat
Perkalian dan pembagian adalah operasi matematika yang lebih kompleks dibandingkan penjumlahan dan pengurangan. Perkalian adalah proses pengulangan penjumlahan, sedangkan pembagian adalah proses mencari berapa kali satu bilangan bulat dapat dikurangi dari bilangan bulat lainnya.
Sifat-sifat Perkalian dan Pembagian: Aturan yang Mengatur Operasi
Perkalian dan pembagian bilangan bulat juga memiliki beberapa sifat penting, yaitu:
- Sifat Komutatif Perkalian: Urutan perkalian tidak memengaruhi hasilnya. Misalnya, 2 x 3 = 3 x 2.
- Sifat Asosiatif Perkalian: Cara mengelompokkan bilangan dalam perkalian tidak memengaruhi hasilnya. Misalnya, (2 x 3) x 4 = 2 x (3 x 4).
- Sifat Distributif Perkalian terhadap Penjumlahan: Perkalian suatu bilangan dengan jumlah dua bilangan sama dengan jumlah perkalian bilangan tersebut dengan masing-masing bilangan. Misalnya, 2 x (3 + 4) = (2 x 3) + (2 x 4).
- Sifat Identitas Perkalian: Perkalian bilangan bulat dengan 1 menghasilkan bilangan bulat itu sendiri. Misalnya, 5 x 1 = 5.
- Sifat Invers Perkalian: Setiap bilangan bulat non-nol memiliki invers perkalian, yaitu bilangan bulat yang jika dikalikan dengannya akan menghasilkan 1. Misalnya, invers perkalian dari 5 adalah 1/5, karena 5 x (1/5) = 1.
Bilangan Bulat dalam Kehidupan Sehari-hari: Penerapan yang Tak Terbatas
Bilangan bulat bukan hanya konsep matematika abstrak, tetapi juga memiliki peran penting dalam kehidupan sehari-hari. Dari mengukur suhu hingga menghitung uang, bilangan bulat membantu kita memahami dan mengatur dunia di sekitar kita.
Ngomongin soal bilangan bulat, pasti langsung inget pelajaran matematika jaman sekolah dulu. Nah, di blog UI An Nur Lampung ini, kamu bisa belajar lebih dalam tentang konsep, operasi, dan penerapan bilangan bulat. Tapi, tahukah kamu kalau konsep bilangan bulat juga bisa diaplikasikan dalam kehidupan sehari-hari?
Misalnya, ketika kamu membeli barang, kamu pasti mempertimbangkan nilai guna barang tersebut, yaitu seberapa bermanfaat barang itu untukmu. Nilai Guna Barang ini bisa diukur dengan berbagai cara, salah satunya dengan membandingkan harga dan kualitas barang. Nah, ternyata, kemampuan menghitung dan membandingkan nilai guna barang ini juga melibatkan konsep bilangan bulat, lho! Jadi, belajar bilangan bulat nggak cuma buat nilai ujian bagus, tapi juga berguna buat hidup kamu!
Menghitung Suhu: Mengukur Kedinginan dan Kepanasan
Bilangan bulat digunakan untuk mengukur suhu, baik dalam derajat Celcius maupun Fahrenheit. Suhu di atas titik beku air diwakili oleh bilangan bulat positif, sedangkan suhu di bawah titik beku air diwakili oleh bilangan bulat negatif. Misalnya, suhu 25 derajat Celcius menunjukkan cuaca yang panas, sedangkan suhu -5 derajat Celcius menunjukkan cuaca yang dingin.
Mengatur Keuangan: Menghitung Pendapatan dan Pengeluaran
Bilangan bulat digunakan untuk mengatur keuangan, seperti menghitung pendapatan, pengeluaran, dan saldo bank. Pendapatan biasanya diwakili oleh bilangan bulat positif, sedangkan pengeluaran diwakili oleh bilangan bulat negatif. Saldo bank yang positif menunjukkan saldo yang tersedia, sedangkan saldo bank yang negatif menunjukkan saldo yang minus.
Menentukan Ketinggian: Mengukur Jarak Vertikal
Bilangan bulat digunakan untuk menentukan ketinggian, seperti ketinggian gunung, ketinggian pesawat terbang, atau ketinggian bangunan. Ketinggian di atas permukaan laut diwakili oleh bilangan bulat positif, sedangkan ketinggian di bawah permukaan laut diwakili oleh bilangan bulat negatif. Misalnya, Gunung Everest memiliki ketinggian 8.848 meter di atas permukaan laut, sedangkan Laut Mati memiliki ketinggian 430 meter di bawah permukaan laut.
Mencatat Waktu: Mengatur Kehidupan dengan Jam
Bilangan bulat digunakan untuk mencatat waktu, seperti jam, menit, dan detik. Waktu biasanya diwakili oleh bilangan bulat positif. Misalnya, pukul 10:30 pagi diwakili oleh 10 jam dan 30 menit. Bilangan bulat juga digunakan untuk mencatat tanggal, seperti tahun, bulan, dan hari.
Menghitung Skor: Menentukan Pemenang dalam Pertandingan
Bilangan bulat digunakan untuk menghitung skor dalam olahraga, seperti sepak bola, basket, dan tenis. Skor biasanya diwakili oleh bilangan bulat positif. Tim dengan skor tertinggi adalah pemenangnya. Bilangan bulat juga digunakan untuk menghitung jumlah poin, assist, dan rebound dalam olahraga.
Menentukan Lantai Gedung: Mengatur Tata Letak Bangunan
Bilangan bulat digunakan untuk menentukan lantai gedung, seperti lantai dasar, lantai satu, lantai dua, dan seterusnya. Lantai dasar biasanya diwakili oleh bilangan bulat nol, sedangkan lantai di atasnya diwakili oleh bilangan bulat positif. Bilangan bulat juga digunakan untuk menentukan nomor ruangan di setiap lantai.
Bilangan Bulat dalam Matematika Lanjutan: Aplikasi yang Lebih Kompleks
Bilangan bulat bukan hanya konsep dasar dalam matematika, tetapi juga memiliki peran penting dalam matematika lanjutan. Bilangan bulat digunakan dalam berbagai bidang matematika, seperti teori bilangan, aljabar, kriptografi, dan teori graf.
Teori Bilangan: Mempelajari Sifat Bilangan Bulat
Teori bilangan adalah cabang matematika yang mempelajari sifat bilangan bulat, termasuk pembagian, faktor, kelipatan, dan bilangan prima. Teori bilangan memiliki aplikasi dalam kriptografi, ilmu komputer, dan fisika.
Aljabar: Mempelajari Operasi dan Persamaan
Aljabar adalah cabang matematika yang mempelajari operasi dan persamaan yang melibatkan variabel. Bilangan bulat digunakan sebagai konstanta dan koefisien dalam persamaan aljabar. Aljabar memiliki aplikasi dalam berbagai bidang, seperti ilmu komputer, fisika, dan ekonomi.
Kriptografi: Mengiripsi dan Dekripsi Data
Kriptografi adalah ilmu yang mempelajari cara mengamankan informasi dengan menggunakan algoritma matematika. Bilangan bulat digunakan dalam algoritma kriptografi untuk mengiripsi dan dekripsi data. Kriptografi memiliki aplikasi dalam keamanan komputer, komunikasi, dan perbankan.
Teori Graf: Mempelajari Hubungan Antara Objek
Teori graf adalah cabang matematika yang mempelajari hubungan antara objek. Bilangan bulat digunakan untuk mewakili simpul dan sisi dalam graf. Teori graf memiliki aplikasi dalam berbagai bidang, seperti ilmu komputer, ilmu sosial, dan biologi.
Kesimpulan: Bilangan Bulat – Konsep Dasar yang Penting
Bilangan bulat merupakan konsep matematika yang sederhana namun penting. Bilangan bulat digunakan dalam berbagai bidang kehidupan, mulai dari kehidupan sehari-hari hingga matematika lanjutan. Dengan memahami konsep bilangan bulat, kita dapat memahami dan mengatur dunia di sekitar kita dengan lebih baik. Bilangan bulat, meskipun terlihat sederhana, merupakan dasar dari berbagai ilmu pengetahuan dan teknologi yang kita gunakan saat ini.